<Hamstring 이란?>
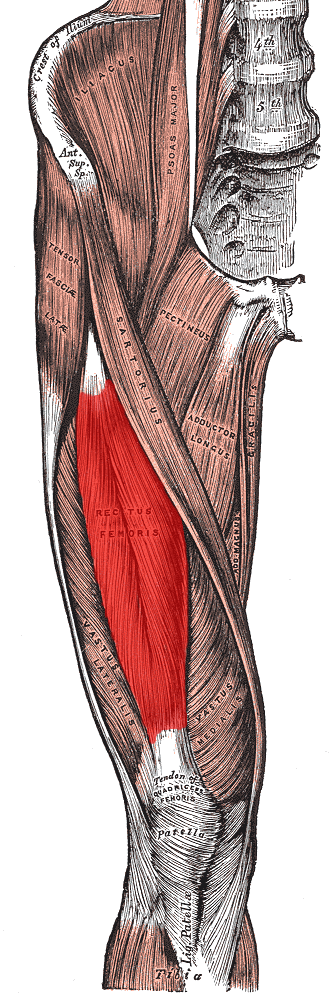
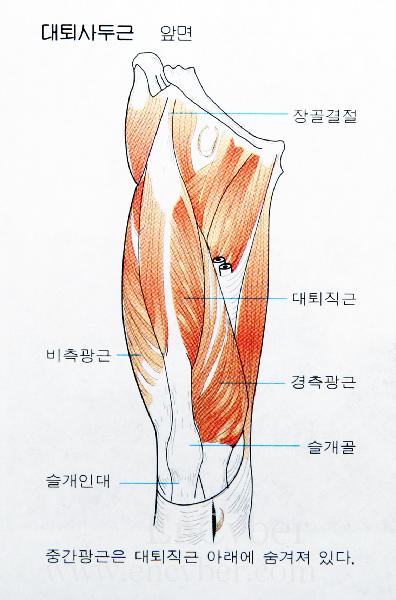
인간의 허벅지를 보면 앞쪽의 근육근과 뒤쪽의 근육근이 있습니다. 앞쪽을 Quadriceps femoris(대퇴사두근) 라고 하여 Rectus Femoris, Vastus Lateralis, Vastus Medialis, Vastus Intermedius입니다. 뒤쪽은 Hamstring 이라고 하여 Biceps femoris, Semitendinosus, Semimembraneous를 지칭합니다. hamstring에서 ham은 '허벅다리 살'을 의미합니다. 우리가 보동 먹는 햄은 돼지허벅다리 살을 의미합니다. string은 끈 이나 선을 의미하는데, 긴 tendon(힘줄)을 가지고 있기 때문에 string이라고 합니다. 합쳐서 햄스트링이란 허벅다리 살과 그와 연결된 힘줄을 의미한다고 보면 됩니다.
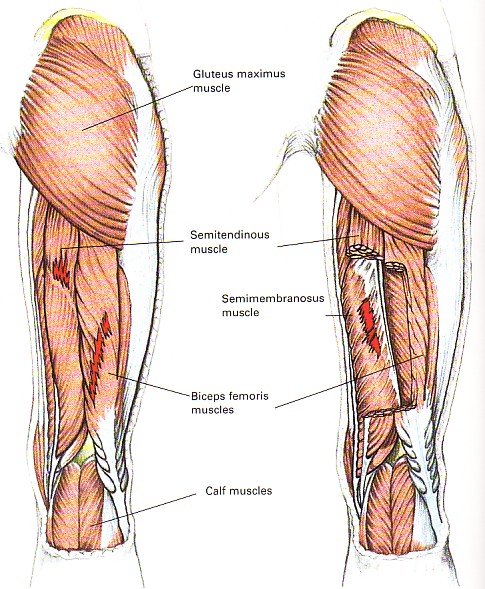

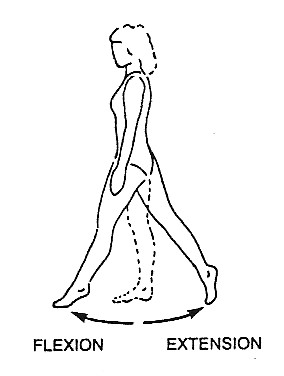
<왜 Hamstring 부상이 자주일어나는가?>
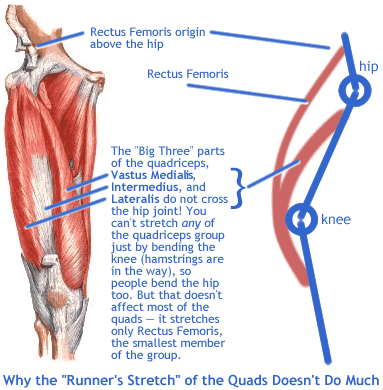
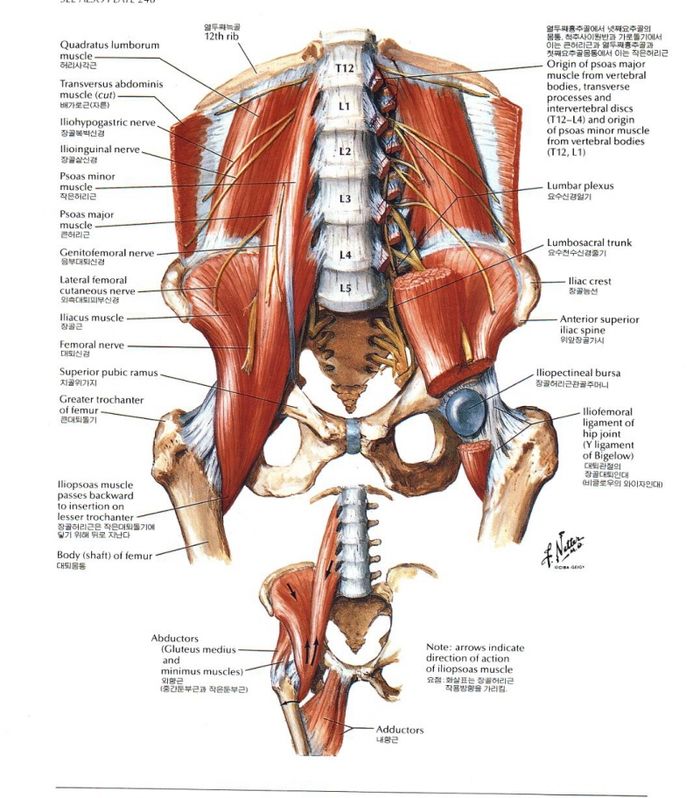
보통 해부학적으로 관절부위의 각도가 줄어드는 것을 flexion, 각도가 커지는 것을 extension으로 정의합니다. 따라서 그림에서 보듯이 일반적으로 고관절은 180도를 유지하는데, flexion이 되면 180도 보다 작고, extension이 되면 180도 보다 큽니다. 마찬가리로 슬관절(무릎)을 볼 때 다리를 펴는 것을 extension, 구부리는 것을 flexion으로 정의합니다. 햄스트링 부상이 자주 발생하는 원인은 2 joint muscle이기 때문입니다. 2 joint muscle이란 한 근육이 2개의 관절에 걸쳐있다는 것입니다. 대표적인 예가 대퇴사두근 중 Rectus femoris와 Hamstring근육들입니다. Rectus femoris는 골반 안쪽에서 시작하여 경골조면(무릎 뼈 밑의 튀어 나온 부위)에서 끝이 나기 때문에 사두근이 수축을 하게되면, 고관절은 flexion이되고, 무릎은 extension이 됩니다. 반면, 햄스트링은 골반 뒤쪽에서 시작하여 뒷 무릎 밑의 경골(tibia) 뒤쪽에서 끈나기 때문에 근육이 수축할 경우 고관절은 extension이 되고, 무릎부위는 flexion이 발생합니다.
쪼그리고 앉았다가 일어나는 행위를 살펴 봅시다. 고관절은 extension이 일어나야 하고, 무릎관절은 extension이 일어나야합니다. 앞서 언급했듯이 고관절 extension을 위해서는 햄스트링이 수축을 해야하는데, 햄스트링이 수축을 하게되면 저절로 무릎관절은 flexion이 되어야 합니다. 하지만, 일어서기 위해서는 무릎관절은 extension이 발생해야 하기 때문에 사두근의 수축이 발생해야 합니다. 그러나, 사두근의 수축을 고관절의 flexion을 일으키기 때문에 일어서는 행위(고관절의 extension)에 반대하는 행위를 유발합니다. 이것은 전문 용어로는 Lombard's paradox라고 합니다. 우리가 간단히 아무 생각없이 쪼그리고 앉았다가 일어나는 행동을 하지만, 근육내에서는 무척 복잡하게 일어나면 서로가 두 관절부위에서 반대되는 행위를 유발하기 때문에 힘이 센 근육이 이깁니다. 사두근이 더 큰 근육이고 힘이 세기 때문에 보통은 사두근의 수축이 발생한 후 햄스트링의 수축이 발생하는 식으로 서로 타협을 하며 조화롭게 움직입니다.
하지만, 때에 따라서는 갑작스러운 달리기 출발, 갑작스럽게 앉은 상태에서 일어나는 경우, 갑작스럽게 공을 차려는 순간등에서 사두근과 햄스트링 사이에 타협을 하지 않고 서로 힘자랑을 할 경우, 아니면 운동신경명령이 잘 되지 않아 동시에 수축하려는 경우 부상이 발생합니다. 앞서 언급했듯이 사두근이 더 힘센 근육이기 때문에 같이 수축하여 힘자랑 할 경우 늘 햄스트링이 다치게 됩니다. 그래서, 우리가 보통 축구나 갑작스런 달리기나 추진력을 요하는 운동에서 햄스트링 부상이 쉽게 발생합니다.
또 하나의 문제는 보통 사람들이 운동전 워밍업을 할 때 햄스트링 부위의 스트레칭은 등한 시 하기 때문에 경기 중 부상을 많이 당합니다. 또한 지속적인 운동으로 근육에 피로가 누적될 경우는 neuromuscular control이 잘 되지 않기 때문에 부상의 위험이 있을 수 있습니다.
<햄스트링 부상 부위와 치유>
보통 햄스트링 부상시 근육과 힘줄이 만나는 부분의 파손이 많이 발생합니다. 즉 뒤쪽 엉덩이 깊숙한 부분이나 뒷 무릎부분입니다. 왜냐면, 근육에 강한 부하가 걸릴 경우 근육이 감당하기 힘든 상황에서는 힘줄이 감당을 하는데, 그보다 더 큰 부하가 걸릴 경우는 힘줄 부위의 파손이 이루어집니다. 보통 부상 순간, 갑작스런 "욱"하는 통중을 느끼거나 "뚝"하고 끊어지는 느낌을 받게 됩니다. 부상 후는 허벅지 뒤쪽의 심한 통증과 걷기가 불편해 집니다. 왜냐면 무릎은 굽히는 행동과 허벅지를 뒤어 옮기는 행동이 자유롭지 못하기 때문입니다. 근육의 파열이 일어나는 경우도 있지만, 많은 경우 힘줄 부위에 부상이 있습니니다. 때로는 부상 후 부상 부위를 만져보면 물렁물렁하다는 것을 느낄 수 있으며, 며칠이 지나면 시퍼렇게 멍든 것처럼 부상부위의 피부색이 변할 수도 있습니다. 자세한 진단은 MRI를 통해서 가능하고, X-ray를 통해서는 뼈의 이상유뮤를 관찰하기 때문에 근육이나 힘줄의 이상을 찾아내기 거의 힘듭니다.
부상 후 3~5일 간은 잘대적인 안정이 필요하며, 그 후에는 조금씩 스트레칭을 해 주면서(아프지 않을 정도) 조금씩 회복운동을 해 주어야 합니다. 근육의 부분파열일 경우 보통 한달 정도면 되는데, 힘줄부위의 파열의 경우 적게는 수개월에서 1년에 걸쳐야 회복이 되는 경우도 있습니다. 보통은 6개월로 보기도 합니다. 특히 위쪽 힘줄부위 부상(엉덩히 깊숙한 곳)은 재활이 제대로 이루어지지 않을 경우 만성이 될 가능성이 많습니다. 박찬호 선수의 경우 햄스트링 부상을 얕보고 완전히 회복되지 않은 상태에서 무리를 하다가 재차 부상을 당한 경우입니다. 그 후 구단에서는 박선수의 의사와 상관없이 긴 치유기간을 거치도록 조치를 취했습니다. 힘줄 부위(그림에서 흰색부위)의 부상은 회복이 매우 더딥니다. 왜냐면 피가 잘 통하기 않기 때문에 면역기능은 하는 요소들이 그 부위를 잘 갈 수가 없습니다. 그래서, 근육부위 부상보다 더 긴 시간이 필요합니다. 심하게 파열된 경우는 기브스를 해야하고 완전히 파열된 경우는 수술을 통해야 합니다.
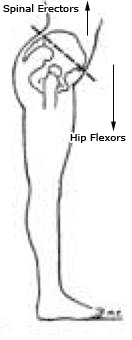
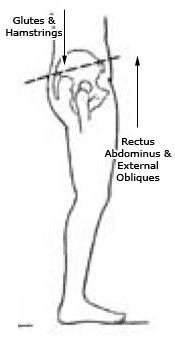
Lombard's paradox
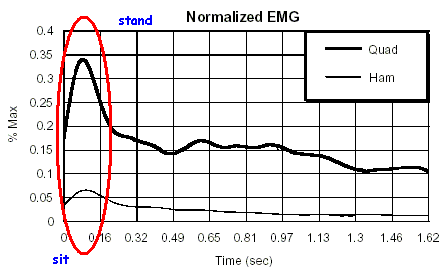
Palpate the quadriceps and hamstring muscles as you arise to standing from sitting. These muscle groups are simultaneously active as a subject arises from sitting, even though the rectus femoris and the hamstrings are antagonistic. This very real coactivation of two antagonistic muscles during the activity of standing from a sitting position has been known for many years as Lombard's paradox (Lombard & Abbott, 1907).
The paradox is classically explained by noting the relative moment arms of the hamstrings and rectus femoris at either the hip or the knee, and their effects on the magnitude of the moments produced by either muscle group at each of the two joints (Rasch & Burke, 1978, pp. 296-7).
Muscles cannot develop different amounts of force in their different parts. The hamstrings, for instance, cannot selectively extend the hip without acting with equal force at the knee. Thus, the only way for hip extension and knee extension to occur simultaneously in the act of standing (or eccentrically in the act of sitting) is for the net moment to be an extensor moment at both the hip and knee joints.
How does a net hip extension moment result when antagonistic muscles develop both extensor and flexor moments at the same time? All that is necessary is for the hip extensor moment to exceed the hip flexor moment. Two antagonistic muscles can produce such a net moment, even if they develop identical forces, if their moment arms around the hip are unequal. In this standing activity, the hamstrings' moment arm with respect to the hip joint's lateral axis exceeds that of the rectus femoris.
Similarly, a net knee extensor moment results at the knee even though the hamstrings and rectus femoris develop simultaneous and antagonistic moments. All that is necessary is for the knee extensor moment to exceed the knee flexor moment. The antagonists produce a net knee extension moment, even if they develop identical forces, because their moment arms around the knee are unequal; the rectus femoris' moment arm at the knee exceeds that of the hamstrings.
The phenomenon still interests students of biomechanics (Gregor, Cavanagh, & LaFortune, 1985). Whatever its explanation, the fact that the hamstrings and quadriceps are simultaneously active at the knee during closed chain activities is a factor in the design of rehabilitation programs.
References:
Gregor, R.J., Cavanagh, P.R., & LaFortune, M. (1985). Knee flexor moments during propulsion in cycling--a creative solution to Lombard's Paradox. Journal of Biomechanics, 18, 307-16 .
Lombard, W.P., & Abbott, F.M. (1907). The mechanical effects produced by the contraction of individual muscles of the thigh of the frog. American Journal of Physiology, 20, 1-60.
Rasch, P.J., & Burke, R.K. (1978). Kinesiology and applied anatomy. (6th ed.). Philadelphia: Lea & Febiger.
--------------------------------------------------------------------------------
Last updated 2-8-01 ⓒDave Thompson PT
http://moon.ouhsc.edu/dthompso/namics/lombard.htm
Lombard's Paradox describes a paradoxical muscular contraction in humans. When standing up from a sitting position, both the hamstrings and quadriceps contract at the same time. However, these muscle groups are antagonistic, meaning that they should not contract at the same time.
The rectus femoris biarticular muscle acting over the hip has a smaller hip moment arm than the hamstrings. However, the rectus femoris moment arm is greater over the knee than the hamstring knee moment. This means that contraction from both rectus femoris and hamstrings will result in hip and knee extension. Hip extension also adds a passive stretch component to rectus femoris, which results in a knee extension force. This paradox allows for efficient movement, especially during gait.
http://en.wikipedia.org/wiki/Lombard's_Paradox
 |  |
www.realbodywork.com/
 |  |
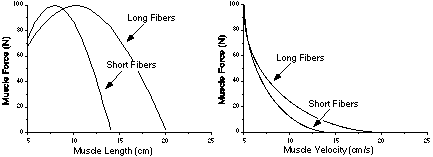
Different Fiber Lengths
Let us consider the effects of architecture using an example of two muscles with identical PCSAs and pennation angles but different fiber lengths. Before reading ahead, try to draw the appropriate length-tension and force-velocity curves.
As shown below, the effect is to increase the muscle velocity (or, stated identically, to increase the muscle excursion). The peak absolute force of the length-tension curves is identical, but the absolute muscle active range is different. That sounds a lot like active range of motion (ROM), a measurement that is extremely important in clinical evaluation. In fact, it is directly related to ROM--ROM is a direct result of muscle architecture and the joint properties on which the muscle acts.
For the same reason that fiber length increases the active muscle range of the length-tension relationship, it causes an increase in the muscle's absolute maximum contraction velocity (Vmax). Again, while the fiber length increase causes an increase in these extrinsic properties, it has no effect on the intrinsic properties of the muscle. A similar exercise can be performed comparing muscles with different PCSAs and fiber lengths. Try predicting force-velocity and length-tension curves for the case where both architectural parameters are changed.
회전축의 중심에서 힘의 작용선 까지의 수직거리를 나타내며 모멘트팔(moment arm)이라 부른다.
Joint Moment Arm
Although muscles produce linear forces, motions at joints are all rotary. The rotary torque is the product of the linear force and the moment arm or mechanical advantage of the muscle about the joint's center of rotation. Mechanically, this is the distance from the muscle's line of action to the joint's center of rotation.
Determination of joint moment arm requires an understanding of the anatomy and movement (kinematics) of the joint of interest. For example, some joints can be considered to rotate about a fixed point. A good example of such a joint is the elbow. At the elbow joint, where the humerus and ulna articulate, the resulting rotation occurs primarily about a fixed point, referred to as the center of rotation. In the case of the elbow joint, this center of rotation is relatively constant throughout the joint range of motion. However, in other joints (for example the knee) the center of rotation moves in space as the knee joint rotates because the articulating surfaces are not perfect circles. In the case of the knee, it is not appropriate to discuss a single center of rotation--rather we must speak of a center of rotation corresponding to a particular joint angle, or, using the terminology of joint kinematics, we must speak of the instant center of rotation (ICR), that is, the center of rotation at any "instant" in time or space.
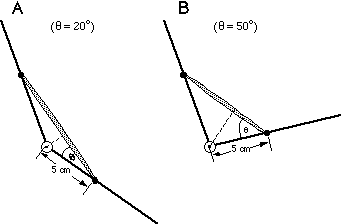
Having defined a joint ICR, the moment arm is defined as the perpendicular distance from line of force application to the axis of rotation. This is illustrated for a simulated elbow joint. In A, the elbow joint is almost fully extended. Let the angle, q, between the brachialis muscle and the ulna be relatively small, e.g., q=20°. Let the distance between the brachialis insertion site and the elbow instant center be 5 cm. In this case, the perpendicular distance between the line of force application and the elbow ICR is shown by the dotted line in A and is equivalent to 5 cm x sin(20°) = 1.7 cm. Thus because the joint is nearly fully extended, this presents an unfavorable mechanical advantage to the muscle--the moment arm is relatively small. Much of the force generated by the muscle will simply compress the joint, not rotate it. Contrast this situation with the conditions shown in B, where the joint has now been flexed so that q=50°. Now, the moment arm equals 5 cm x sin(50°) = 4.3 cm. We see that for a simple hinge joint (a joint with a fixed ICR), the maximum moment arm is attained at q=90°. If we plotted moment arm vs. joint angle for this simple hinge joint, we would obtain a simple sine function that has a maximum of 5 cm occurring at q=90°. Such a curve can be generated for any joint. In general, the experimental curves are not quite as simple as the one here.
Muscle-Joint Interactions
Maximum Strength
Examination of current physiology texts reveals a good deal of wishy-washiness regarding the definition of the joint angle that corresponds to maximum strength. Typically, it is stated that muscle force is maximum when the joint is in a neutral position, or when the muscle is at resting length. What is the basis for such statements? Unfortunately, there is very little scientific basis for such a statement. Recent studies of torque generation in animals and humans have generally agreed that the joint angle at which the muscle generates maximal force is not the same angle at which moment arm is maximum. Thus, during normal joint rotation, both moment arm and muscle force are constantly changing which results in the "shape" of the strength or torque curve. This concept has recently been addressed in detail by experimental and theoretical modeling (Hoy et al., 90; Lieber and Boakes, 1988; Lieber and Shoemaker, 1992). What an interesting design!
Range of Motion as a Function of Architecture
We can now "combine" the muscle architectural discussion with the joint moment arm concept. We stated that muscles with longer fibers have a longer functional range than muscles with shorter fibers (Muscle Architecture). Does this imply that muscles with longer fibers are associated with joints that have larger ROMs? The answer is No. It is true that a muscle with longer fibers does have a longer working range. However, the amount of muscle length change that occurs as a joint rotates is very strongly dependent on the muscle's moment arm--the perpendicular distance from the muscle insertion to the axis of joint rotation.
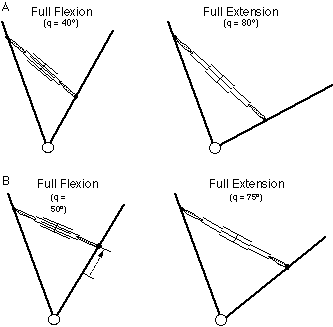
This indicates that muscles that appear to be designed for speed because of their very long fibers may not actually produce large velocities if they are placed in position with a very large moment arm. The increased moment arm causes a greater joint moment, and the muscle may actually be better suited for isometric torque production. Similarly, a muscle that appears to be designed for force production due to a large PCSA, if placed in position with a very small moment arm, may actually produce high joint excursions or angular velocities. Thus, muscle design may or may not be a reflection of its actual use in the physiologic torque-generating system. It does seem, in general, that muscle fiber length and muscle moment arm are positively correlated (McClearn, 1985). Thus muscles with long fibers tend to have long moment arms, but this need not necessarily be the case. Muscle architectural features may represent muscle adaptation to kinematic criteria. However, definitive answers to these suggestions await further study.
References
- Hoy, MG, Zajac, FE, and Gordon, ME. A musculoskeletal model of the human lower extremity: the effect of muscle, tendon, and moment arm on the moment-angle relationship of musculotendon actuators at the hip, knee, and ankle. J. Biomech. 1990;23:157-169.
- Lieber, RL, and Boakes, JL. Sarcomere length and joint kinematics during torque production in the frog hindlimb. Am. J. Physiol. 1988;254:C759-C768.
- Lieber RL, and Shoemaker, SD. Muscle, joint, and tendon contributions to the torque profile of frog hip joint. Am. J. Physiol. 1992;263:R586-R590.
- McClearn, D. Anatomy of raccoon (Procyon lotor) and caoti (Nasua narica and N. nasua) forearm and leg muscles: relations between fiber length, moment-arm length, and joint excursion. J. Morphol. 1985;183:87-115.
http://muscle.ucsd.edu/musintro/fl.shtml
http://muscle.ucsd.edu/musintro/ma.shtml
http://muscle.ucsd.edu/musintro/interaction.shtml
Trackback URL : 이 글에는 트랙백을 보낼 수 없습니다
Trackback RSS : http://www.fallight.com/rss/trackback/1567
Trackback ATOM : http://www.fallight.com/atom/trackback/1567







